Расчёт кварцевых фильтров Гаусса
Jack Smith, K8ZOA
Из журнала QEX May/June 2007 pp. 16…20
Критичными узлами панадаптера Z90, описанного в апрельском/майском номерах журнала QEX за 2007 г, являются два кварцевых фильтра. Поскольку требования к фильтру панадаптера отличаются от требований, предъявляемых к кварцевым фильтрам, применяемым в приёмниках для приёма CW и SSB, и поскольку дело разработки фильтра часто неверно относят к уделу “чёрной” магии, рассмотрим расчёт фильтра более детально. Несмотря на то, что речь здесь пойдёт о фильтрах Гаусса, процедура идентична для фильтров любого типа.
Перед тем как сосредоточиться на расчёте фильтров, описываемом здесь, я изготовил более дюжины экспериментальных кварцевых фильтров с центральными частотами от 3,58 до 13,5 МГц. Основываясь на полученном опыте, я строю свои расчёты относительно недорогих кварцевых резонаторов от микропроцессорных плат вычислительной техники, выпускаемых фирмой ECS, Inc. International (www. ecsxtal.com). Я применил изделие ECS-80-S-1X 8,0 с номинальной рабочей частотой 8,0 МГц. Расчёт начинаем с выбора требуемой полосы пропускания, типа АЧХ и количества звеньев.
Полоса пропускания. Конечная получаемая полоса пропускания является критерием при изготовлении кварцевого фильтра. В нашем случае, будем рассматривать “узкий” и “широкий” фильтры.
Промышленные аналоговые анализаторы спектра обеспечивают автоматический выбор полосы пропускания в пределах примерно 0,3%...2% от полного диапазона перекрываемых частот. Чтобы обеспечить анализ SSB сигнала – обычная задача, которую призван исполнять панадаптер, достаточно иметь диапазон перекрываемых частот в 10 кГц. Этим обусловливается полоса пропускания “узкого” фильтра - 30…200 Гц. Опытная работа с недорогими “микропроцессорными” кварцевыми резонаторами показала, что получить полосу уже 200 Гц с ними проблематично из-за ограничений, связанных с добротностью резонаторов, так что примем “узкую” полосу нашего фильтра равной 200 Гц. Чем уже полоса фильтра, тем медленнее должна быть развёртка АЧХ, чтобы избежать амплитудных и частотных ошибок.
Также входящим в выбор полосы пропускания Z90 является и количество выборок – анализируемых точек по горизонтали, число которых установим равным 240. Чтобы избежать амплитудных ошибок, АЧХ фильтра по уровню - 3 дБ должна быть значительно более широкополосной, чем расстояние между двумя точками анализа. При диапазоне равном 20 кГц, расстояние между точками анализа составляет 83,3 Гц. При диапазоне 200 кГц (± 100 кГц), между точками анализа расстояние будет составлять 833 Гц. Поэтому для использования в качестве “широкого” фильтра, подойдёт таковой с полосой пропускания в 1 кГц, хотя можно было б взять чуть-чуть и пошире. Возможно, более важно, как показывает практика, как только полоса пропускания фильтра становится намного большей 1 кГц при этих кварцевых резонаторах на 8,0 МГц, при нашей простой топологии схемы, исчезает симметрия. Отсюда и остановимся на полосе пропускания “широкого” фильтра в 1 кГц.
Тип АЧХ фильтра. Манипулируя плоскостью формы АЧХ, крутизной её ската и другими параметрами, разработчики фильтров создали множество их разновидностей (многие получили в названиях имена создателей). Так появились фильтры Баттерворта, Чебышева, Бесселя, Гаусса…Фильтры Гаусса и подобные им традиционно применяются в анализаторах спектра или панадаптерах (панорамных индикаторах). Фильтры Гаусса обеспечивают оптимальную амплитудную характеристику при качании частоты генератора плавно или с помощью импульсов. (Реальный фильтр Гаусса для его реализации требует бесконечное множество элементов, наш четырёх-звенный фильтр имеет приближённую к Гауссовской характеристику, количество расчётных точек более чем достаточно).
Количество звеньев. Увеличение количества звеньев фильтра приводит к улучшению его селективности, повышению крутизны спада АЧХ, увеличению подавления сигналов за пределами полосы пропускания фильтра. Однако, увеличение количества звеньев фильтра повышает и требования к качеству элементов его составляющих, точности подбора компонентов и их согласованию между собой. Так, например, в Z90 используется четырёх-звенный фильтр. Стандартным источником информации при создании фильтров, обычно, является “Справочник по синтезу фильтров” Зверева, в которой говорится, что 4-звенный фильтр Гаусса имеет полосу пропускания по уровню - 60 дБ в 10 раз большую, чем при уровне - 3 дБ, так что коэффициент прямоугольности фильтра составит 10 : 1. (В анализаторах спектра традиционно используется отношение - 3 дБ : - 60 дБ, вместо часто встречающегося в радиолюбительской практике соотношения - 6 дБ : - 60 дБ). Если мы применим даже десяти-звенный фильтр Гаусса, коэффициент прямоугольности улучшится не более, чем до 4,8 : 1.
Характеристики применяемых кварцевых резонаторов. Невозможно изготовить фильтр с заданными параметрами, не зная характеристик элементов его составляющих, здесь: кварцевых резонаторов. Как отмечал Максвелл (James Clerk Maxwell), в честь которого было названо уравнение, лет этак 130 назад: “Наиболее важным аспектом любого явления, с математической точки зрения, является насколько оно будет измерено количественно”.
Лорд Кельвин разделял эти взгляды: “Если Вы можете измерить то, о чём говорите и выражаете это в цифрах, то Вы знаете о чём говорите; если же Вы не можете измерить этого и не можете выразить этого в цифрах, то Ваши знания скудны и неудовлетворительны, что можно отнести к начальной стадии познания, едва ли их можно признать выдающимися по отношению к состоянию науки…”
На Рис. 1 показана упрощённая практическая модель (эквивалентная схема) кварцевого резонатора.

Рис. 1
Она содержит 4 элемента: Ch – ёмкость кварцедержателя, включая и ёмкость покрытий, нанесённых на обе стороны кварцевой пластины; Cm – динамическая ёмкость; Lm - динамическая индуктивность; Rm – динамическое сопротивление. Параметры Cm, Lm, Rm – названы динамическими (motional) потому, что они являются лишь эквивалентными физическим величинам (вибрациям) кварцевого элемента, другими словами: они являются результатом движения кварцевой пластины, Lm , при этом, соответствует массе пластины, Cm – эластичности, а Rm – потерям на трение. (В профессиональной литературе Ch представлена как Co и динамические параметры: CI, LI, RI). Тем не менее, казалось бы, - виртуальные, параметры Cm, Lm и Rm могут быть измерены и реальны для нас, как и отдельные физические: конденсатор, катушка индуктивности, резистор. Однако, это совсем не означает, что, сняв защитный корпус – экран с кварцевого резонатора, мы обнаружим крошечные детали: конденсатор, катушку индуктивности, резистор. В лучшем случае, мы обнаружим тоненький диск кварцевой пластины с нанесёнными на него с обеих сторон обкладками.
Параметры, указанные на Рис. 1, могут быть измерены различными методами. Сравним три из них:
- Получение параметров путём измерения ёмкости кварцедержателя, частот последовательного и параллельного резонанса.
- Использование метода сдвига частоты генератора, разработанный G3UUR.
- Сравнение этих двух методов с данными (в координатах усиление - фаза), полученными на анализаторе спектра HP87510A для кварцевого резонатора автоматически.

Рис. 2. Изменения импеданса и фазы при последовательном и параллельном резонансах
Ёмкость кварцедержателя. Перед измерением динамических параметров измерим ёмкость кварцедержателя. Хотя мы не будем использовать в уравнениях параметр Ch в нашем случае с узкополосным фильтром, тем не менее, этот параметр очень важен при более сложных расчётах, например, для более широкополосных фильтров, как о том говорится в классических трудах Dishal по теме.
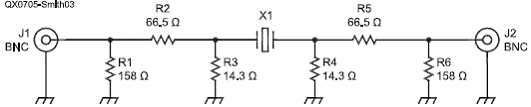
Рис. 3. Резистивная П-образная схема для измерения параметров резонаторов
Мы встречаем также параметр Ch в некоторых методологиях для вычисления динамических параметров кварцевых резонаторов. Поэтому важно измерить ёмкость Ch как можно точнее. Для того, чтобы не путать параметр Ch с динамическими, измеряем эту ёмкость на частотах много меньших резонансной для резонатора. Плодом моих трудов в этом направлении явилась Таблица 1, в которой сведены результаты измерений ёмкости кварцедержателя.
Таблица 1
- Измерения ёмкостей кварцедержателей
- Способ Значение Комментарий
- Цифровой измеритель ёмкости 3,7 пФ прибор DCM-601
- Разрешение 0,1 пФ
- Анализатор HP87510A 4,13 пФ на частоте 100 кГц
- 3,89 пФ на частоте 300 кГц
- 3,83 пФ на частоте 1 МГц
- 3,90 пФ на частоте 2 МГц
- Измеритель добротности HP4342A
- с катушкой 2,5 мГн методом сдвига резонанса 3,85 пФ на частоте 145 кГц
- Усреднено 3,83 пФ за исключением 4,13 пФ
Кроме значения 4,13 пФ, (примем как исключение), среднюю ёмкость кварцедержателя можно вычислить из оставшихся пяти измерений, она составит 3,83 пФ.
Метод последовательного и параллельного резонанса. Если мы включим кварцевый резонатор между сигнал – генератором и амплитудным детектором (измерителем амплитуды на выходе), то, изменяя частоту генератора в небольших пределах от указанной на корпусе резонатора, обнаружим два резонанса. Первый даст максимум показаний на выходе детектора и соответствует частоте последовательного резонанса или частоте, на которой резонируют Cm и Lm (которые образуют последовательный резонансный контур). Если мы настроим сигнал-генератор немного выше по частоте, то обнаружим минимум показаний измерителя амплитуды, а виной тому будет резонанс Ch с комбинацией CmLm, составляющих параллельный колебательный резонансный контур. Если производить измерения на соответствующей аппаратуре, то можно измерить и сдвиг фазы, - на обеих частотах (последовательного и параллельного резонанса) сдвиг фазы равен 0°. На Рис. 2 показано изменение амплитуды и фазы, в зависимости от частоты, для резонатора частотой 8 МГц, применяемом в нашем случае при расчёте фильтра.
Измерения в нашем случае проводились с использованием измерителя усиления и фазы HP87510A - векторного анализатора, работающего в диапазоне частот 100 кГц…300 МГц, оптимизированного для измерения параметров компонентов, включая измерение и автоматический расчёт и индикацию эквивалентных параметров кварцевых резонаторов. HP87510A сочетает в себе функции сигнал-генератора и детектора как амплитудного, так и фазового с измерителем. Методы, которыми мы будем пользоваться, применимы к широкому спектру измерительной аппаратуры. Посмотрите труды Hayward’а и Pivnichny, по методам испытания, не требующим изощрённой измерительной аппаратуры. Даже, в случае применения анализатора, придётся не просто подключать кварцевый резонатор к порту прибора, а вставить его в испытательную схему, чтобы он был в реальных эксплуатационных условиях по импедансу, уровню возбуждения, в некоторых случаях (но не в нашем), параллельно резонатору необходимо ещё и подключить конденсатор. Хоть у меня и не было специального кварцедержателя, рекомендуемого для применения с анализатором HP41900A, можно было что-то придумать подобное на замену, способное обеспечить достаточную точность при подборе резонаторов для кварцевых фильтров. (Будем считать достижимую малую величину паразитной ёмкости самодельного кварцедержателя включенной параллельно, которая лишь увеличивает ёмкость Ch, влияя на достижимую точность измерений и расчётов).
Стандартом IEC предусмотрено: при испытании, кварцевый резонатор должен быть от источника с выходным импедансом 12,5 Ом и нагружен таким же сопротивлением – 12, 5 Ом. Это традиционно сопровождается и П-образными резистивными звеньями аттенюатора, включенными тыльными сторонами (back-to-back) для обеспечения согласования с 50-омной измерительной аппаратурой, что, однако, выражается в затухании полезного сигнала, равного 29, 6 дБ. Посмотрите труды Salt’а или Pivnichny. Принципиальную схему моей версии аттенюатора, с применением резисторов с 1% допуском, можно видеть на Рис. 3, а внешний вид на Рис. 4.

Рис. 4. Вид на печатную плату резистивного П-образного согласователя
На Рис. 5 можно увидеть, как подключается опытное устройство к анализатору HP87510А.
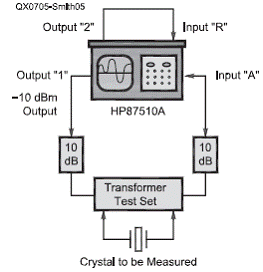
Рис. 5. Схема испытательного устройства для измерения параметров кварцевых резонаторов с использованием анализатора HP87510A
Аттенюаторы по 10 дБ (модель CAT-10) на входе и выходе измерительной схемы позволяют доводить импедансы портов схемы до требуемых 12,5 Ом, характеристических для кварцевого резонатора. (Некоторые данные были получены мной на трансформаторной согласующей схеме 50 : 12,5 Ом ранее, но та схема работала с большей погрешностью, чем резистивная).
Также важно использовать в тест-схеме те же уровни, на которых будет работать резонатор в родной схеме, поскольку динамические параметры резонаторов изменяются в зависимости от уровня раскачки, явление, известное в индустрии как “зависимость от уровня возбуждения” (DLD). (Также возможно резонатор и вывести из строя (разрушить пластинку кварца), если подать на него чрезмерный уровень возбуждения). Все данные по тестированию кварцевых резонаторов были сняты при уровне возбуждения - 20 дБм, приложенного к испытательной схеме.
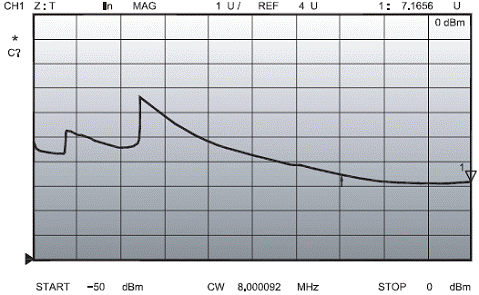
Рис. 6. Изменение последовательного сопротивления (Rm) кварцевого резонатора в зависимости от уровня его возбуждения. Отметьте скачкообразный характер изменения этого параметра
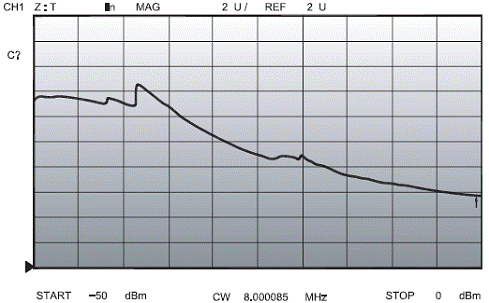
Рис. 7. Второй кварцевый резонатор показал такую же зависимость
На рисунках 6 и 7, например, показано значительное изменение Rm, при изменении уровня раскачки от - 50 дБм до 0 дБм. (В этом случае, звенья аттенюатора - 10 дБ не применялись). Оба кварца показали изменение Rm скачками, причём, просматривалась тенденция к уменьшению этого параметра с ростом амплитуды возбуждения. Чтобы проверить, являются ли скачки артефактами инструментальными или это проявление тестируемых резонаторов, включенных в схему, я установил плёночный резистор сопротивлением 9,1 Ом (0,25 Вт) вместо резонатора, характеристика которого показана на Рис. 6.
На Рис. 8 приведена характеристика опытной схемы, где кварцевый резонатор замещён резистором, как видно, никаких скачков, в этом случае, при изменении амплитуды раскачки от - 50 до 0 дБм, не обнаружено, что говорит о том, что в “производстве скачков” повинен кварцевый резонатор. Salt в своих трудах описывает скачки амплитуды, подобные, приведённым на Рис. 6 и Рис.7 , как результат взаимодействия различных резонансов (видимо, от различных измерений кварцевой пластины, да и последовательный-параллельный резонансы кварцевого резонатора– UA9LAQ), которые сдвигаются по частоте (в различной степени), при малейшем изменении режима возбуждения кварцевой пластины. К счастью, эти резонансы различаются по частоте лишь на немного. Cm и Lm также немного изменяют свои параметры при изменении уровня возбуждения. (Вот почему кварцевые фильтры могут быть источником интермодуляции за счёт изменения динамических параметров резонаторов при изменении уровня возбуждения).
Вставив кварцевый резонатор в испытательную схему, измерим 4 параметра, а если позволяет измерительная аппаратура, то и пятый:
- Частоту последовательного резонанса – fs
- Частоту параллельного резонанса – fp
- Полосу пропускания (по уровню – 3 дБ) при последовательном резонансе – Δf
- Паразитная ёмкость кварцедержателя в испытательной схеме – Cp
- Последовательное затухание на резонансной частоте - α
На Рис. 9 и Рис. 10 показаны графики функции от частоты для кварцевого резонатора ECS-80-S-1X 8,0 МГц, из которых мы получаем данные для Таблицы 2. Значение паразитной ёмкости (Cp) измерено отдельно. Последующий анализ динамических параметров кварцевого резонатора основан на Инструкции по применению лаборатории Omicron. Согласно стандартной теории схем, сначала определим частоты последовательного и параллельного резонансов, а также добротность кварцевого резонатора, выраженные в параметрах резонатора:
![]()
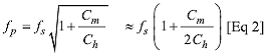
![]()
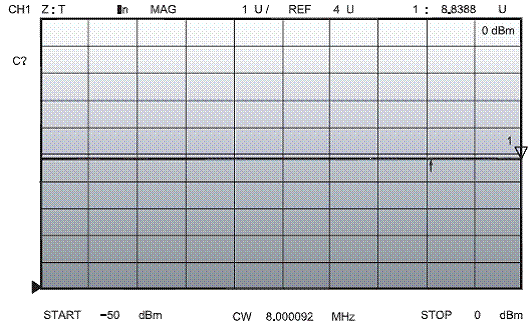
Рис. 8
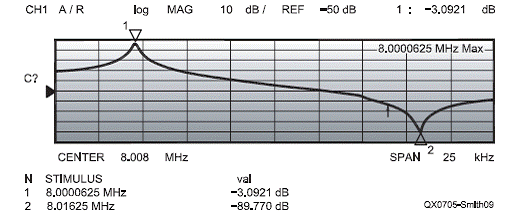
Рис. 9
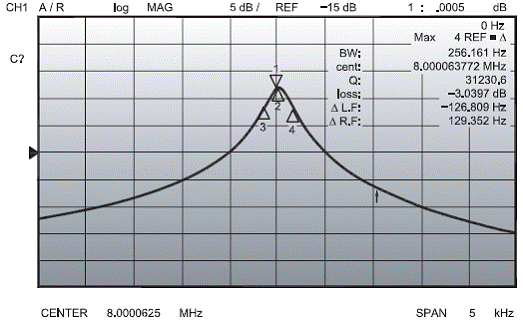
Рис. 10
Поскольку эти параметры измеряются с кварцевым резонатором, вставленным в измерительную схему, мы должны к действующей ёмкости кварцедержателя добавить и паразитную ёмкость монтажа, чтобы найти фактическую ёмкость подключения – Ch adj:
![]()
Приводим данные уравнения для поиска динамических параметров в соответствие с нашими данными параметрами – fs, fp, Ch и QL:
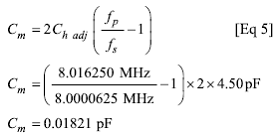

Вычисляем QL, нагруженную добротность кварцевого резонатора:
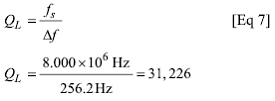
Таблица 2
Измеренные параметры кварцевого резонатора ECS-80-S-1X 8,0 МГц
Параметр Значение
- fs 8,0000625 МГц
- fp 8,0162500 МГц
- Δf 256,2 Гц
- Cp 0,67 пФ
- α 3,1 дБ
Из определения Q находим последовательное сопротивление Rtotal, которое “видит” кварцевый резонатор, состоящее из Rm плюс сопротивления источника и нагрузки.
![]()
Решая уравнение получаем:
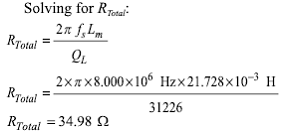
Сопротивления источника и нагрузки равны по 12,5 Ом, которые мы вычтем из Rtotal, чтобы получить Rm:
![]()
Возможно ли определение динамических параметров без знания ёмкости кварцедержателя и паразитной ёмкости схемы подключения резонатора? Ответ утвердительный – да.
На Рис. 10 указано измеренное затухание α = 3,0397 дБ. Примем это значение за истинное и, конечно же, не стоит принимать даже такую точность, как четыре знака после запятой, чтобы вычислить все четыре параметра: нагруженную добротность – Q и, следующую из неё индуктивность Lm, а также импедансы источника и нагрузки:
Зависимость между последовательным сопротивлением и затуханием:
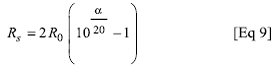
- где: Rs – последовательное сопротивление;
- Ro – импеданс источника и нагрузки, принятые равными друг другу;
- α – затухание в децибелах
Применив это к нашим данным измерений, определяем динамическое сопротивление:
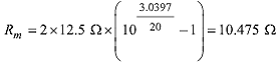
Полное сопротивление, которое “видит” Lm составляет 10,475 Ом плюс импедансы источника и сопротивление нагрузки по 12,5 Ом, что даёт 35,475 Ом.
Найдём Lm:
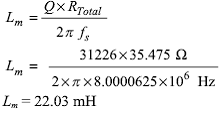
Cm может быть определена из частоты последовательного резонанса:
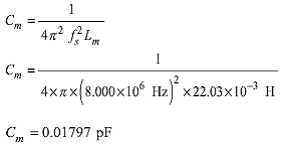
По правде говоря, эти расчёты не дают об ёмкости кварцедержателя и о точном значении затухания, а также об импедансах источника и нагрузки.
Мы должны бы, хотя бы, ради принципа иметь возможность измерить импедансы источника и нагрузки с такой же точностью как ёмкость кварцедержателя и паразитную ёмкость испытательной схемы.
Метод G3UUR. David Gordon Smith – G3UUR разработал метод определения параметров кварцевых резонаторов, описанный Wes’ом Hayward’ом. Этот метод заключается в измерении сдвига частоты генератора Колпитца при подключении последовательно с кварцевым резонатором конденсатора небольшой ёмкости. Параметры Lm и Cm вычисляются из следующих уравнений:
![]()
- где, Cs – ёмкость последовательно включенного конденсатора;
- Δf – изменение частоты, при введении дополнительного конденсатора;
- Lm определяется по резонансной частоте из уравнения 6 (Eq 6):
Таблица 3
Частоты кварцевого резонатора ECS-80-S-1X 8,0 МГц измеренные по методу G3UUR
Условие Значение
- Без конденсатора 8,000613 МГц
- С последовательно включенным конденсатором 8,002418 МГц
- Сдвиг частоты 1805 Гц
Свободный перевод с английского: Виктор Беседин (UA9LAQ)